arrowspace-rs: Faster (not approximate?) Nearest Neighbours
You can find arrowspace in the:
- Rust repository ↪️
cargo add arrowspace - and Python repository ↪️
pip install arrowspace
This is an important release as it comes after the confirmation received on the previous post and focus on making those results replicable giving the computation a solid backup in numerical stability, the core of the computation is available in this file.
In particular I am now quite convinced that arrowspace is one of the fastest Approximate Nearest Neigbours algorithm out there and as far as the test goes also not approximate, as it returns the same results as cosine similarity. Obviously backing this from a single-researcher perspective will take much more time and effort.
According to the time-complexity computation and based on public knowledge of other algorithms:
- "training" phase (index building) with complexity:
O(n * d * k * log(n)). The latest comparative benchmark achieves index building on 310,000 records dataset at ~1600s (single machine, 12 cores). This involves graph building and linear score computation; - "inference" phase (index lookup for similar vectors):
O(n * log(n * k)), this is the usual complexity for search on a sorted set.
This was possible because of the improvements described in the previous post and because the hardening of tests that made evident some limitations in the sampling strategy, now improved and better tested, and the clustering algorithm, now made more consistent (see below). In particular I would like to mention: pre-filtered clustering to top-k neighbours with a new smartcore’s CosineSimilarity structure based on my implementation of FastPair, an approach to clustering using inline-sampling, a procedure that allows spotting optimal k-number of clusters using a mix of statistical approximations (K-means-Lloyd, Calinski-Harabasz score for Between-Group Sum of Squares and Within-Group Sum of Squares).
As you see I am starting to think the index in terms of Machine Learning principles as few far-fetched ideas sprung from this latest effort; in particular how to do graph learning on the feature graph currently used and how to use taumode in a potential cost function or something on the same wave.
For now let’s focus on this version:
What’s new in v0.16.0
Deterministic clustering
With a controllable seed enables stable runs and reproducible search behavior across builds, removing prior sources of variability in graph construction.
A configurable sampling
Sampling strategy was added and SimpleRandomSampler is now the default beside the alternative AdaptiveSampler; both simplifies scaling larger corpora without sacrificing recall in the tail, with AdaptiveSampler making clustering a little less deterministic in exchange for some time savings.
Parallel clustering computation
It was a challenge to make the row-by-row computation working with deterministic sequential for-loop and with a parallel for-loop at the same time. Version 0.15.0 was somehow flaky in terms of consistency of clustering results, code available here. Since the beginning I had this idea of doing clustering and sampling in the same loop, I don’t know if it is a common thing, it helps in daving a for-loop on potentially very large datasets.
To ensure replicable builds it is not possible to use a parallel iterator in clustering for the obvious reason that we will get different clustering outcome. It was improved and made seed‑aware for both clustering and spectral search paths, aligning throughput with determinism goals. This is particularly useful in the explorative phase of a graph and in tests, when the parameters are not being fully identified correctly.
Furthermore, tests were strengthened and flakiness removed to lock in numeric stability as part of CI. Still one or two tests fail for a particular architecture but the problems have been mitigated
Run context
The same as the previous article. The CVE experiment reused the same three analyst‑style queries as before and computed cosine (τ=1.0), hybrid (τ=0.8), and taumode (τ=0.62) over a shared candidate set, allowing like‑for‑like NDCG and tail statistics, see previous post.
Per‑query rank agreement in v0.16.0 is perfect across Spearman, Kendall, and NDCG@10, indicating the spectral modes re‑weight the tail without disturbing the head ordering for the tested queries.
Headline results
Average NDCG@10 is 1.0000 for both “Hybrid vs Cosine” and “Taumode vs Cosine,” reflecting identical top‑k order for these queries under v0.16.0. Average Tail/Head ratios improve as τ drops below 1.0, with taumode showing the strongest long‑tail quality and the lowest tail variability.
Version comparison
The table below places the previously reported v0.15.0 snapshot next to v0.16.0 on the same evaluation axes used in earlier posts.
| Metric | v0.15.0 | v0.16.0 |
|---|---|---|
| Avg NDCG@10 (Hybrid vs Cosine) | 0.9988 | 1.0000 |
| Avg NDCG@10 (taumode vs Cosine) | 0.9886 | 1.0000 |
| Avg Tail/Head ratio (Cosine) | 0.9114 ± 0.0463 | 0.9718 ± 0.0019 |
| Avg Tail/Head ratio (Hybrid) | 0.9394 ± 0.0340 | 0.9787 ± 0.0012 |
| Avg Tail/Head ratio (taumode) | 0.9593 ± 0.0259 | 0.9843 ± 0.0008 |
By diagrams:
| CVE Top-10 comparative analysis for the three test queries | |
|---|---|
| Version 0.15 | Version 0.16 |
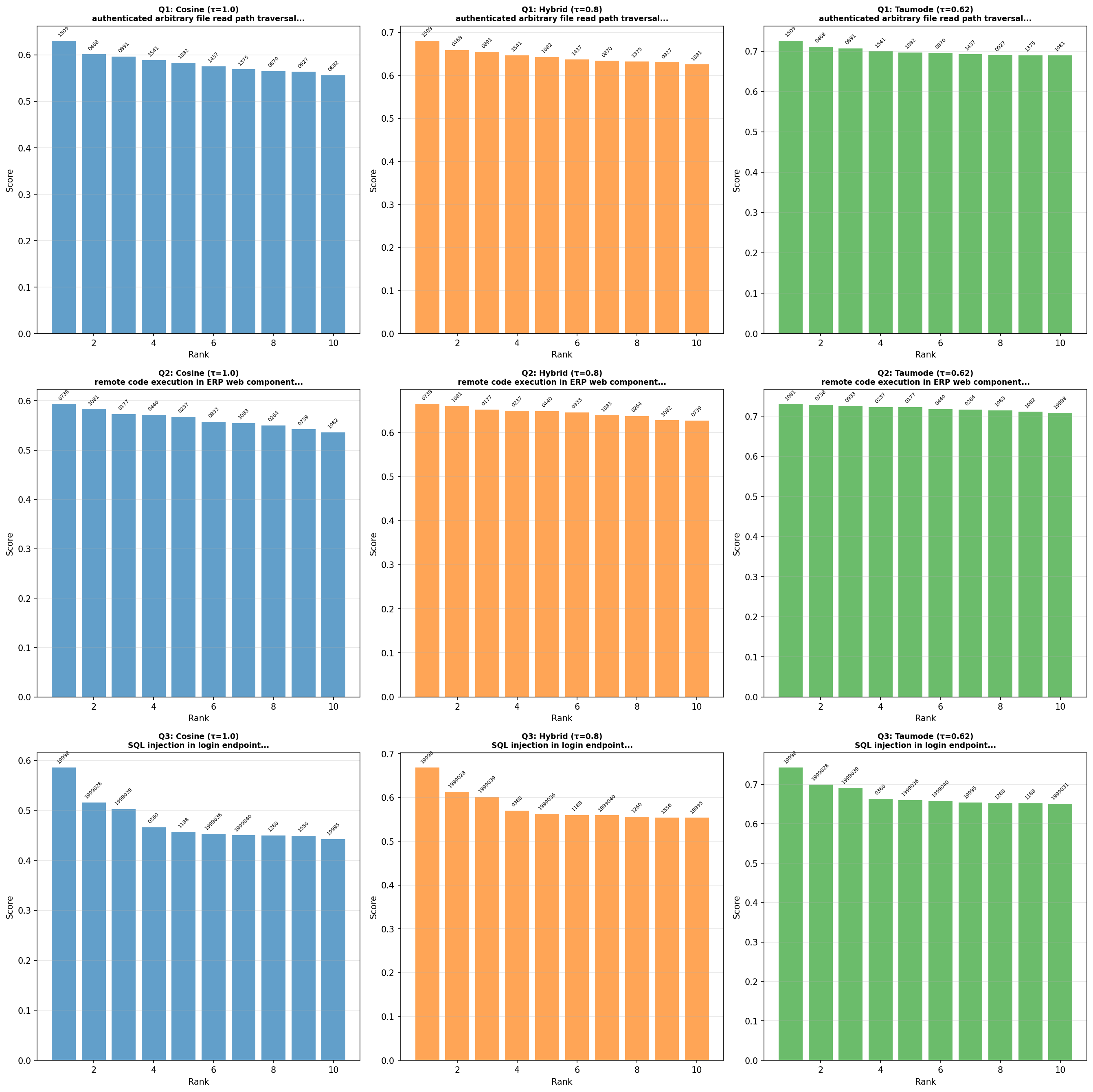
|
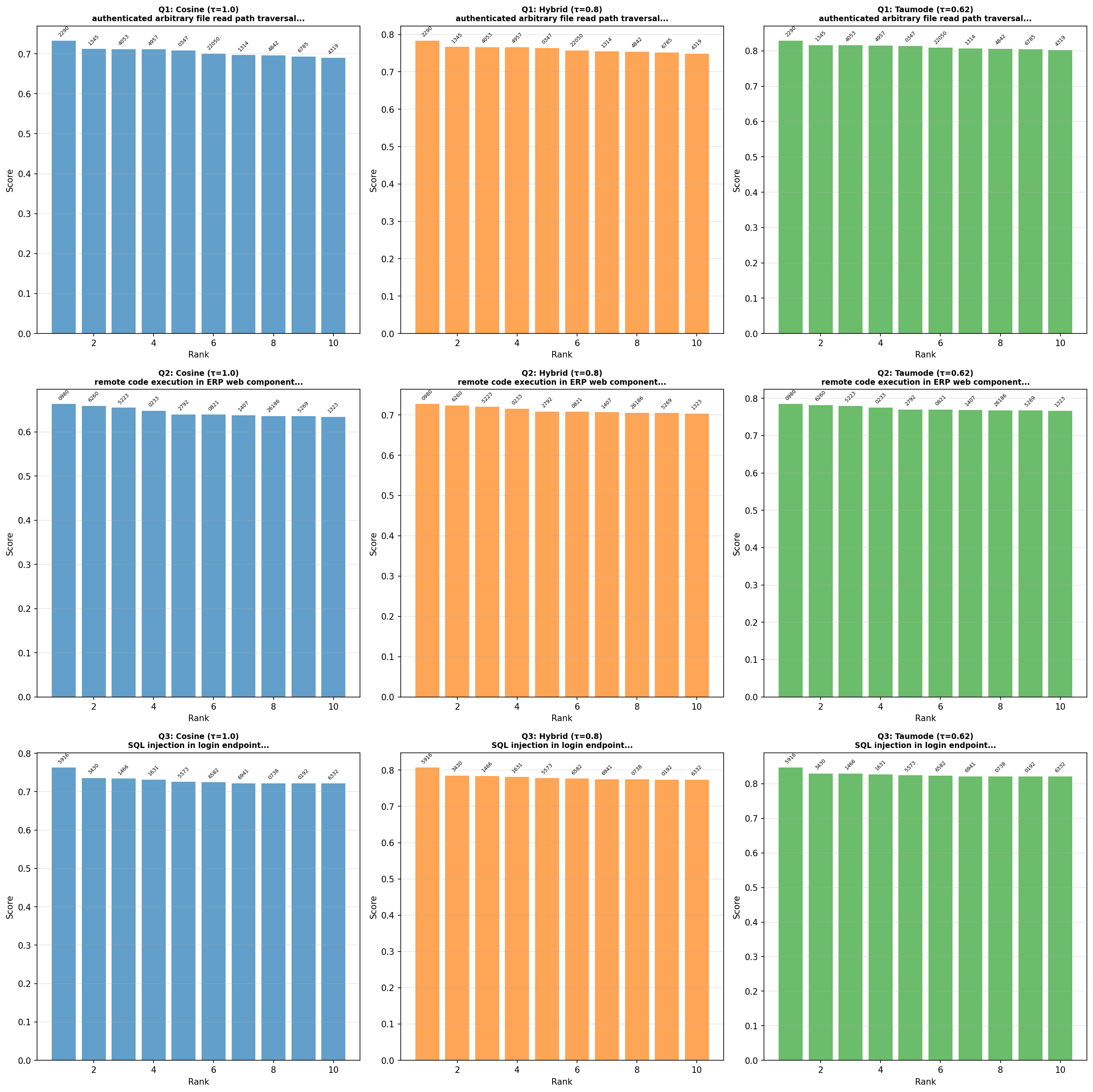
|
| CVE Head/Tail analysis | |
| Version 0.15 | Version 0.16 |
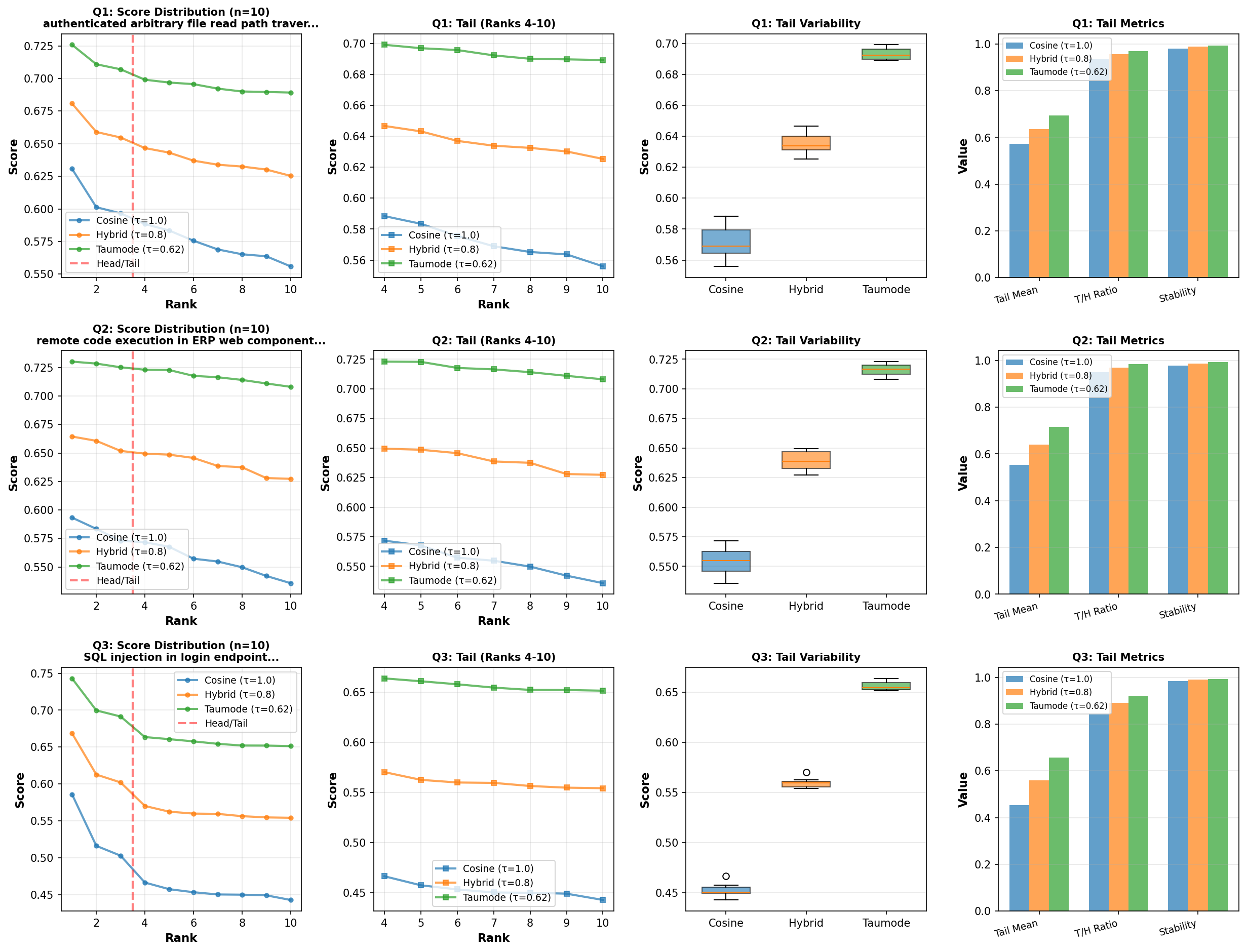
|
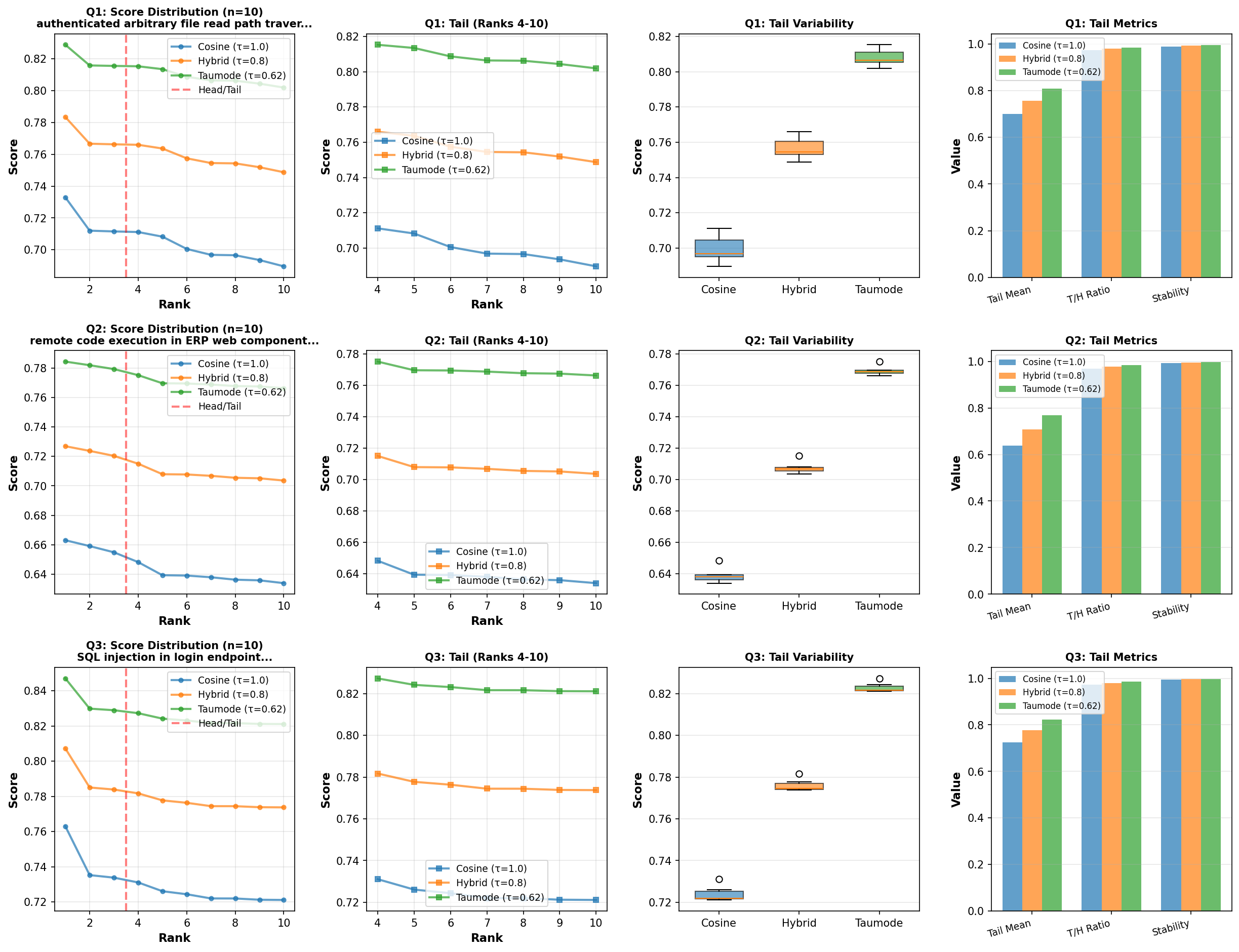
|
Results
taumode is ready to provide additional features and to step up tests to a cloud environment-scale. I may decide to make the CVE dataset searching capability publicly available thorugh an API. If you are interested in such feature, please consider sponsoring my Github. I am self-funded independent researcher.
Interpreting the deltas
Moving from v0.15.0 to v0.16.0, NDCG@10 rises to 1.0000 across both spectral modes, confirming head‑alignment while still boosting tail strength.
Tail/Head ratios tighten substantially and tail coefficients of variation drop for τ<1.0, quantifying the stability and long‑rank consistency improvements attributable to the improvements in clustering algorithm.
Per‑query tail quality
Across the three queries, the tail mean rises and dispersion falls as τ decreases, with taumode achieving the highest tail‑to‑head balance and the lowest CV in each case. This behavior matches the intended “temperature‑like” control in the spectral family, trading a strictly geometric score for one that encodes graph topology while keeping the head intact.
Practical impact
Determinism plus stronger long‑tail stability makes results easier to audit and compare across runs, an important property for operational retrieval and analyst workflows.
Combined with the new default sampler, v0.16.0 shortens iteration time on larger corpora while preserving the spectral signal that lifts tail relevance.
Artifacts
- Top‑10 comparison and tail analysis figures for
v0.16.0were regenerated for the three queries to mirror the earlier post’s layout and scale. - CSV artifacts include per‑query rank correlations and NDCG, tail metrics, and a compact summary for roll‑up reporting.
Next steps
- Build a storage layer for
parquetfiles using Apache Arrow - explore subgaphs and subvector spaces
- Run algebraic analysis on the interval of Reals generated by the characteristic Taumode of each dataset
- Add all the harness required by cloud installations
Interested in learning more? Whether you’re evaluating ArrowSpace for your data infrastructure, considering sponsorship, or want to discuss integration strategies, please check the Contact page.
Please consider sponsoring my research and improve your company’s understanding of LLMs and vector databases.
Book a call on Calendly to discuss how ArrowSpace can accelerate discovery in your analysis and storage workflows, or discussing these improvements.